Effective Python: R-Style Regression
I use R, but I love Python. However, let’s face it, basic linear regression in R is very straightforward. A few clear and intuitive lines of R code produce textbook1 output that is informative and complete. This post compares building and analyzing simple linear regression models in R and Python.
Sample data set
Let’s look at the data set Earnings.txt2 from the Data and Story Library. DASL is a great resource for test data. Earnings.txt includes the price, SAT, ACT, and graduate earnings for over 700 US colleges. .
Exploring the connection between the cost of college and future earnings is interesting in its own right and the post includes more models than needed for the R/Python comparison—I can’t resist—but the outputs are in the Appendix.
1. Ingestion and basic EDA
1.1. Ingestion and basic EDA in R
library(tidyverse)
# College cost vs earnings
df = read_tsv('C:/Users/steve/S/Teaching/2019-01/ACT3349/data/earnings.txt')
dfa = df %>% select(Price, Earn, SAT, ACT, Public)
head(dfa)
# A tibble: 6 x 5
# Price Earn SAT ACT Public
# <dbl> <dbl> <dbl> <dbl> <dbl>
# 1 61300 62800 1510 33 0
# 2 28100 59000 1380 30 1
# 3 64800 62900 1510 34 0
# 4 58600 63700 1460 33 0
# 5 35700 60300 1360 30 1
# 6 18500 51800 1260 29 1
summary(dfa)
# Price Earn SAT ACT Public
# Min. :16500 Min. :28300 Min. : 810 Min. :15.00 Min. :0.0000
# 1st Qu.:25900 1st Qu.:41100 1st Qu.:1040 1st Qu.:23.00 1st Qu.:0.0000
# Median :44000 Median :44750 Median :1120 Median :25.00 Median :0.0000
# Mean :42200 Mean :45598 Mean :1142 Mean :24.98 Mean :0.3796
# 3rd Qu.:55500 3rd Qu.:48900 3rd Qu.:1220 3rd Qu.:27.00 3rd Qu.:1.0000
# Max. :70400 Max. :79700 Max. :1550 Max. :34.00 Max. :1.00001.2. Ingestion and basic EDA in Python
import pandas as pd
# df = pd.read_csv('http://www.mynl.com/static/data/earnings.txt', sep='\t')
df = pd.read_csv('C:/Users/steve/S/Teaching/2019-01/ACT3349/data/earnings.txt', sep='\t')
dfa = df[['Price', 'Earn', 'SAT', 'ACT', 'Public']]
dfa.head()
# Price Earn SAT ACT Public
# 0 61300 62800 1510 33 0
# 1 28100 59000 1380 30 1
# 2 64800 62900 1510 34 0
# 3 58600 63700 1460 33 0
# 4 35700 60300 1360 30 1
dfa.describe()
# Price Earn SAT ACT Public
# count 706.000 706.000 706.000 706.000 706.000
# mean 42,200 45,598 1,142 24.982 0.379603
# std 15,727 6,724 136.572 3.451 0.485632
# min 16,500 28,300 810.000 15.000 0.000
# 25% 25,900 41,100 1,040 23.000 0.000
# 50% 44,000 44,750 1,120 25.000 0.000
# 75% 55,500 48,900 1,220 27.000 1.000
# max 70,400 79,700 1,550 34.000 1.0001.3 Comparison
Neutral. I like getting standard deviation. Obviously, you’d do more EDA! Number formatting was not normalized.
2. Regression
2.1. Regression in R
m1 = lm(data=dfa, Earn ~ Price)
summary(m1)
# Call:
# lm(formula = Earn ~ Price, data = dfa)
#
# Residuals:
# Min 1Q Median 3Q Max
# -16905.1 -4183.1 -921.5 3217.7 30777.6
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 4.042e+04 6.951e+02 58.150 < 2e-16 ***
# Price 1.227e-01 1.544e-02 7.948 7.55e-15 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 6446 on 704 degrees of freedom
# Multiple R-squared: 0.08234, Adjusted R-squared: 0.08103
# F-statistic: 63.17 on 1 and 704 DF, p-value: 7.552e-152.2. Regression in Python
m1 = smf.ols(formula='Earn ~ Price', data=df)
res1 = m1.fit()
res1.summary()
# OLS Regression Results
# ==============================================================================
# Dep. Variable: Earn R-squared: 0.082
# Model: OLS Adj. R-squared: 0.081
# Method: Least Squares F-statistic: 63.17
# Date: Wed, 09 Feb 2022 Prob (F-statistic): 7.55e-15
# Time: 10:39:37 Log-Likelihood: -7193.2
# No. Observations: 706 AIC: 1.439e+04
# Df Residuals: 704 BIC: 1.440e+04
# Df Model: 1
# Covariance Type: nonrobust
# ==============================================================================
# coef std err t P>|t| [0.025 0.975]
# ------------------------------------------------------------------------------
# Intercept 4.042e+04 695.108 58.150 0.000 3.91e+04 4.18e+04
# Price 0.1227 0.015 7.948 0.000 0.092 0.153
# ==============================================================================
# Omnibus: 114.947 Durbin-Watson: 1.232
# Prob(Omnibus): 0.000 Jarque-Bera (JB): 207.069
# Skew: 0.977 Prob(JB): 1.09e-45
# Kurtosis: 4.794 Cond. No. 1.29e+05
# ==============================================================================2.3. Comparing R and Python regression code
- Call syntax: identical
- Extra
.fit()call could be included in the model,res1 = smf.ols(formula='Earn ~ Price', data=df).fit() - Output: comparable, though Python missing the residual standard error. It is available as
res1.scale ** 0.5(from GLMs where the scale acts like the variance).
My verdict: a tie.
3. Plotting
3.1. Plotting in R
require(gridExtra)
gp1 = ggplot(data=dfa, aes(x=Price, y=Earn, col=factor(Public))) + geom_point() + geom_smooth(method='lm')
gp2 = ggplot(data=dfa, aes(x=Price, y=Earn, col=SAT)) + geom_point() + geom_smooth(method='lm')
grid.arrange(gp1, gp2, ncol=2)
3.2. Plotting in Python
import matplotlib.pyplot as plt
fig, axs = plt.subplots(1, 2, figsize=(10, 3.5), tight_layout=True)
ax0, ax1 = axs.flat
ax = ax0
pred_ols3 = res3.get_prediction()
df['iv_l'] = pred_ols3.summary_frame(alpha=0.01)["mean_ci_lower"]
df['iv_u'] = pred_ols3.summary_frame(alpha=0.01)["mean_ci_upper"]
df['fit'] = res3.fittedvalues
x = df.Price
y = df.Earn
df.plot.scatter(x='Price', y='Earn', s=2, marker='o', c=df.Public, ax=ax, colorbar=False)
df.plot.scatter(x='Price', y='fit', s=2, marker='o', c=df.Public, ax=ax, colorbar=False)
df.plot.scatter(x='Price', y='iv_l', s=2, marker='o', c=df.Public, ax=ax, colorbar=False)
df.plot.scatter(x='Price', y='iv_u', s=2, marker='o', c=df.Public, ax=ax, colorbar=False)
ax.legend()
ax.grid(lw=.25, c='w')
ax = ax1
pred_ols1 = res1.get_prediction()
iv_l = pred_ols1.summary_frame(alpha=0.01)["mean_ci_lower"]
iv_u = pred_ols1.summary_frame(alpha=0.01)["mean_ci_upper"]
df.plot.scatter(x='Price', y='Earn', s=2, marker='o', cmap='RdBu', c=df.SAT, ax=ax)
ax.scatter(x, res1.fittedvalues, s=1, c="r", marker='.', label="OLS fit")
ax.scatter(x, iv_u, s=2, c='b', marker='.', label="OLS 99% mean ci")
ax.scatter(x, iv_l, s=2, c='b', marker='.')
ax.grid(lw=.25, c='w')
ax = fig.axes[-1]
ax.set_title('SAT', fontsize=12)
ax.yaxis.set_major_locator(ticker.MultipleLocator(100))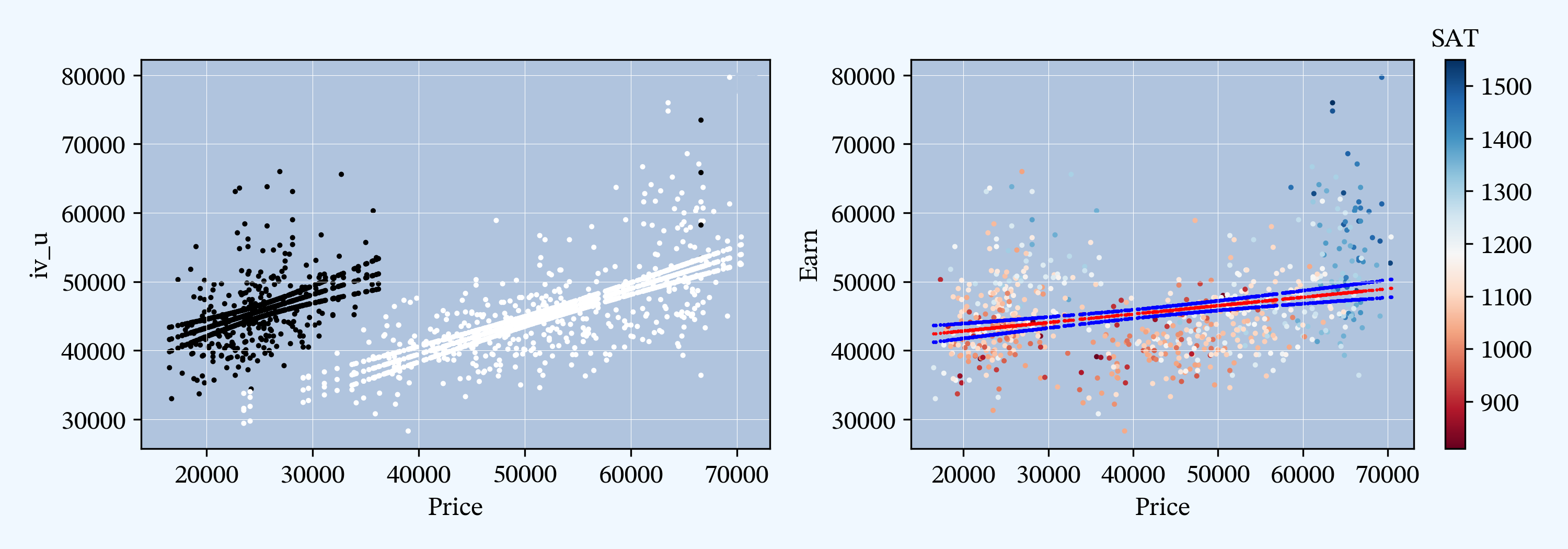
3.3. Comparison
Hummm, why do I love Python so much?
4. Conclusions
Appendix A. More data analysis
Is it worth paying more for a fancy college? Here are a few more model views to consider.
A.1. Further regressions in R
m2 = lm(data=dfa, Earn ~ Price + SAT)
summary(m2)
# Call:
# lm(formula = Earn ~ Price + SAT, data = dfa)
#
# Residuals:
# Min 1Q Median 3Q Max
# -16325.5 -3546.6 -247.4 3202.0 24833.5
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 1.461e+04 1.814e+03 8.055 3.41e-15 ***
# Price 6.177e-03 1.549e-02 0.399 0.69
# SAT 2.691e+01 1.783e+00 15.088 < 2e-16 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 5606 on 703 degrees of freedom
# Multiple R-squared: 0.3068, Adjusted R-squared: 0.3048
# F-statistic: 155.6 on 2 and 703 DF, p-value: < 2.2e-16
m3 = lm(data=dfa, Earn ~ Price * factor(Public))
summary(m3)
# Call:
# lm(formula = Earn ~ Price * factor(Public), data = dfa)
#
# Residuals:
# Min 1Q Median 3Q Max
# -15745 -3827 -552 2699 26268
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 2.039e+04 1.467e+03 13.899 < 2e-16 ***
# Price 4.768e-01 2.737e-02 17.422 < 2e-16 ***
# factor(Public)1 1.322e+04 2.317e+03 5.705 1.71e-08 ***
# Price:factor(Public)1 7.377e-03 7.561e-02 0.098 0.922
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 5502 on 702 degrees of freedom
# Multiple R-squared: 0.3333, Adjusted R-squared: 0.3304
# F-statistic: 117 on 3 and 702 DF, p-value: < 2.2e-16
m4 = lm(data=dfa, Earn ~ Price + factor(Public) + SAT)
summary(m4)
# Call:
# lm(formula = Earn ~ Price + factor(Public) + SAT, data = dfa)
#
# Residuals:
# Min 1Q Median 3Q Max
# -14885 -3365 -377 2924 23955
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 1.050e+04 1.743e+03 6.024 2.75e-09 ***
# Price 2.981e-01 3.217e-02 9.268 < 2e-16 ***
# factor(Public)1 9.355e+03 9.206e+02 10.162 < 2e-16 ***
# SAT 1.661e+01 1.950e+00 8.518 < 2e-16 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 5238 on 702 degrees of freedom
# Multiple R-squared: 0.3957, Adjusted R-squared: 0.3931
# F-statistic: 153.2 on 3 and 702 DF, p-value: < 2.2e-16A.2. Further regressions in Python
m2 = smf.ols(formula='Earn ~ Price + SAT', data=df)
res2 = m2.fit()
res2.summary()
# OLS Regression Results
# ==============================================================================
# Dep. Variable: Earn R-squared: 0.307
# Model: OLS Adj. R-squared: 0.305
# Method: Least Squares F-statistic: 155.6
# Date: Wed, 09 Feb 2022 Prob (F-statistic): 1.14e-56
# Time: 10:39:59 Log-Likelihood: -7094.2
# No. Observations: 706 AIC: 1.419e+04
# Df Residuals: 703 BIC: 1.421e+04
# Df Model: 2
# Covariance Type: nonrobust
# ==============================================================================
# coef std err t P>|t| [0.025 0.975]
# ------------------------------------------------------------------------------
# Intercept 1.461e+04 1814.156 8.055 0.000 1.11e+04 1.82e+04
# Price 0.0062 0.015 0.399 0.690 -0.024 0.037
# SAT 26.9095 1.783 15.088 0.000 23.408 30.411
# ==============================================================================
# Omnibus: 51.603 Durbin-Watson: 1.662
# Prob(Omnibus): 0.000 Jarque-Bera (JB): 80.196
# Skew: 0.541 Prob(JB): 3.85e-18
# Kurtosis: 4.247 Cond. No. 3.87e+05
# ==============================================================================
df["Pubic"] = df["Public"].astype("category")
m3 = smf.ols(formula='Earn ~ Price * Public', data=df)
res3 = m3.fit()
res3.summary()
# OLS Regression Results
# ==============================================================================
# Dep. Variable: Earn R-squared: 0.333
# Model: OLS Adj. R-squared: 0.330
# Method: Least Squares F-statistic: 117.0
# Date: Wed, 09 Feb 2022 Prob (F-statistic): 1.97e-61
# Time: 10:40:27 Log-Likelihood: -7080.5
# No. Observations: 706 AIC: 1.417e+04
# Df Residuals: 702 BIC: 1.419e+04
# Df Model: 3
# Covariance Type: nonrobust
# ================================================================================
# coef std err t P>|t| [0.025 0.975]
# --------------------------------------------------------------------------------
# Intercept 2.039e+04 1466.843 13.899 0.000 1.75e+04 2.33e+04
# Price 0.4768 0.027 17.422 0.000 0.423 0.531
# Public 1.322e+04 2316.891 5.705 0.000 8669.333 1.78e+04
# Price:Public 0.0074 0.076 0.098 0.922 -0.141 0.156
# ==============================================================================
# Omnibus: 123.249 Durbin-Watson: 1.516
# Prob(Omnibus): 0.000 Jarque-Bera (JB): 254.866
# Skew: 0.979 Prob(JB): 4.53e-56
# Kurtosis: 5.198 Cond. No. 5.57e+05
# ==============================================================================
m4 = smf.ols(formula='Earn ~ Price + Public + SAT', data=df)
res4 = m4.fit()
res4.summary()
# OLS Regression Results
# ==============================================================================
# Dep. Variable: Earn R-squared: 0.396
# Model: OLS Adj. R-squared: 0.393
# Method: Least Squares F-statistic: 153.2
# Date: Wed, 09 Feb 2022 Prob (F-statistic): 2.19e-76
# Time: 10:41:24 Log-Likelihood: -7045.7
# No. Observations: 706 AIC: 1.410e+04
# Df Residuals: 702 BIC: 1.412e+04
# Df Model: 3
# Covariance Type: nonrobust
# ==============================================================================
# coef std err t P>|t| [0.025 0.975]
# ------------------------------------------------------------------------------
# Intercept 1.05e+04 1742.734 6.024 0.000 7075.906 1.39e+04
# Price 0.2981 0.032 9.268 0.000 0.235 0.361
# Public 9355.2181 920.576 10.162 0.000 7547.806 1.12e+04
# SAT 16.6125 1.950 8.518 0.000 12.783 20.441
# ==============================================================================
# Omnibus: 80.685 Durbin-Watson: 1.703
# Prob(Omnibus): 0.000 Jarque-Bera (JB): 139.548
# Skew: 0.734 Prob(JB): 4.98e-31
# Kurtosis: 4.610 Cond. No. 4.02e+05
# ==============================================================================Textbook is circular at this point; many textbooks use R output to illustrate!↩︎
Archived copy of the data.↩︎
posted 2022-02-09 | tags: R, regression, Python, Effective Python, matplotlib, statsmodels